13 Wed

TIL

[AI 스쿨 1기] 6주차 DAY 3

출처 : https://github.com/sujiny-tech/k-digital-training-AI-dev/blob/main/Machine-Learning-basics/Linear%20Models%20for%20Classification.md

선형 분류(Linear Classification)

  • 분류 목표 : 입력벡터 x를 K개의 가능한 클래스 중 하나의 클래스로 할당

  • 분류를 위한 결정이론

    • 확률적 모델(probabilistic model)

      • 생성모델(generative model)

        클래스의 사후확률 (using 베이즈 정리) 또는 직접 모델링

      • 식별모델(discriminative model)

        직접 모델링

    • 판별함수(discriminant model)

      확률 계산 없이 입력 x를 클래스로 할당하는 판별함수 구하기(찾기)

판별함수 (Discriminant model)

  • 선형함수에 관한 판별함수에 대해 생각하자.

  • 두개의 클래스에 대한 선형판별함수

    : wight vector

    : bias

    이면 클래스 1로 판별, <0이면 클래스 2로 판별

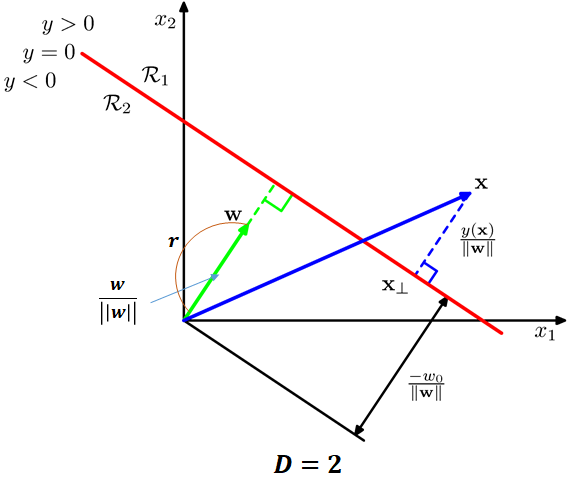
  • 결정 경계(decision boundary)

    • y(x)=0을 만족하는 x의 집합 (x가 D차원의 입력벡터일 때, D-1차원의 hyperplane)

    • 결정 경계면 위

      → 즉, 는 결정경계면에 수직

    • 원점에서 결정 경계면까지의 거리

      • 벡터 x⊥ : 원점에서 결정 경계면에 대한 사영(projection)일 때 (아래 그림 참고)

        이면, 결정 경계면은 원점으로부터 w가 향하는 방향으로 멀어져있음.

        이면, 결정 경계면은 원점으로부터 w가 반대 방향으로 멀어져있음.

        즉, 는 결정 경계면 위치 결정❗

      • x⊥ : 임의의 한점 x의 결정 경계면에 대한 사영일 때

        y(x)는 x와 결정 경계면 사이의 부호화된 거리에 비례

        정리하면,

        이면, x는 결정 경계면 기준으로 w가 향하는 방향에 있음

        이면, x는 결정 경계면 기준으로 -w가 향하는 방향에 있음.

        의 절댓값이 클수록 더 멀리 떨어져있음.

      • (수식 단순화) 가짜입력 dummy input 이용

  • 다수의 클래스에 대한 판별함수

    • 클래스 에 대해 표현하면 다음과 같음.

      일 때, 를 만족하면, x를 클래스 로 판별

분류를 위한 최소제곱법 (Least squares for classification)

  • 사실 분류를 위해 최소제곱법 쓰는건 별로 좋지 x❗

  • 클래스를 판별하는 판별식은 다음과 같음

    행렬 에 대해 나타내면,

    의 k번째 열 :

  • 제곱합 에러 함수(sum-of-squared error function)

    • 학습 데이터 , , n번째항이 인 행렬 T, n번째 행이 인 행렬 이 주어졌을 때, 제곱합 에러함수는 다음과 같음.

    유도 과정은 다음과 같음.

    에 대해 미분하고 식 전개하면,

    ( : pseudo-inverse 행렬)

  • 따라서 판별함수는 다음과 같음.

  • 분류를 위한 최소제곱법의 문제점✨

    • outlier에 민감

    • 목표값의 확률분포에 대한 잘못된 가정에 기초❗

퍼셉트론 알고리즘 (The perceptron algorithm)

  • 기저함수를 넣어 일반화된 식으로 표현하면 다음과 같음.

    여기서 이며, f는 활성함수(activation function)로 계단형 함수임

  • 에러 함수

    : 잘못 분류된 데이터들의 집합

  • Stochastic gradient descent의 적용하면,

  • 위 업데이트가 실행될 때 잘못 분류된 샘플에 미치는 영향

⭐ 최소제곱법과 퍼셉트론 모두 output 출력하지만, 확률을 계산하진 않음❗

확률적 생성 모델 (Probabilistic Generative Models)

  • 모델링 한 다음 → 클래스의 사후확률 을 구함❗ (using 베이즈 정리)

  • 이전 판별함수에서는 에러함수를 최소화하는 최적의 파라미터를 찾는 것이 목적이지만, 확률적 모델은 데이터 분포를 모델링하면서 분류 문제를 결과적으로 풀게됨❗

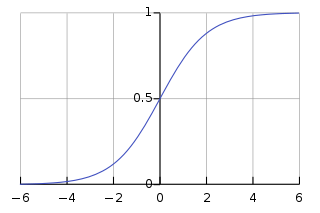
  • 2-class를 가정하고, x가 클래스 1(C1)에 속할 확률

    (a에 관한 logistic sigmoid function)

  • 일반 선형 모델(generalized linear model) - 클래스가 k>2인 경우 (일반화)❗

    • (a에 관한 softmax function)

⭐ 2-class : logistic sigmoid function를 이용, k-class : softmax function를 이용❗

  • 연속적 입력 (continuous inputs)

    • 가 가우시안 분포를 따르고, 모든 클래스에 대해 공분산이 동일하다고 가정하자.

    • 가정 하에 어떤 클래스가 주어졌다면, 해당 데이터를 output하는 확률은 다음과 같음.

    • 2-class에 대해서,

      이때, w벡터와 w0는 다음과 같음.

      a에 대한 전개

    • k-class에 대해서는 다음과 같이 확장 가능.

  • 최대우도해 (Maximum likelihood solution)

    • 2-class의 경우

      • 데이터와 파라미터들

        • 실제 데이터 에 대해 이면 클래스 1로 분류하고, 은 클래스 2로 분류.

        • 라 할때, 구하고자하는 파라미터는 ❗

      • 우도함수

        • 각 클래스에 대해 다음과 같이 표현할수 있음

          p({\bf x}_n, C_2) = p(C_2)p({\bf x}_n|C_2) = (1-\pi) N({\bf x}_n;\mu_2, \Sigma)

          따라서,

        π 구하기μ 구하기∑ 구하기

데이터가 이산일 때 (Discrete features)

  • 각 특성 이 0 또는 1, 하나의 값만 가질 수 있는 경우

    • 클래스가 주어졌을 때 특성들이 조건부 독립(conditional independence)이라는 가정을 할 경우 문제는 단순화됨! → naive Bayes 가정

      이때, 이며, 위 식을 k-class의 에 대입하면 다음과 같음.

      함수가 함수에 대해 선형인 것을 확인할 수 있음.

[Statistics 110]

Present Part [3 / 34]

3강- Birthday Problem과 확률의 특성 (Birthday Problem, Properties of Probability)

생일 문제 : 생일이 같은 두 명의 사람을 찾기

  • 가정

    • 2월 29일은 제외한다

    • 365일이 모두 동일한 확률을 가진다

      • 실제로는 그렇지 않다. 예를 들어 9월에 출생이 많다.

      • 독립 : 한 사람의 생일이 다른 사람의 생일에 영향을 미치지 않는다.

최소한 몇명의 사람이 있어야 50%의 확률을 만족할까?

  • 365개의 상자에 공을 최소한 하나씩 집어넣는 경우와 동일

  • 사람이 366명일 경우는 확률이 1이다.

    • 이를 비둘기집 원리라고 한다

  • 대부분의 사람들은 직관적으로 150~180명을 이야기하며 보통 100을 넘는다.

  • 실제로는 23명이 있을 때 50.7%의 확률을 가진다

모두의 생일이 같지 않을 확률

  • 이를 1에서 빼면 적어도 두 명이 생일이 같을 확률을 구하는 것과 같다

  • P(no match) = 365⋅364⋅  ⋯  ⋅(365−k+1)365k \frac {365 \cdot 364 \cdot \ \ \cdots \ \ \cdot (365 - k + 1)} {365^k} : 365개의 날짜 중 1명이 한 날짜를 차지하면 다른 1명은 남은 364개의 날짜 중 한 날짜를 차지하는 방법

  • P(match)

    • 50.7% if k = 23

    • 97.0% if k = 50

    • 99.999% if k = 100

k에 대한 직관

  • (k2)=k(k−1)2 {k \choose 2} = {k(k-1) \over 2}

  • (232)=23⋅222=253 {23 \choose 2} = {23 \cdot 22 \over 2} = 253

    • 23은 작은 수지만, 23명이 만들 수 있는 쌍의 수는 253개이며 충분히 적어도 한쌍이 생일이 같은지 비교할 수로는 작은 수는 아니다

  • 생일이 같거나 하루 차이 날 확률

    • about 50% if k = 14

확률 정리

  • 기본 정리

    • P(∅\varnothing) = 0, P(S) = 1 and it also means 0≤P(A)≤1 0 \le P(A) \le 1

    • P(∪n=1∞)=∑n=1∞P(An)    if  An  is  disjoint  with  Am(m≠n) P (\cup^\infty_{n=1}) = \sum^\infty_{n=1}P(A_n) \ \ \ \ if \ \ A_n \ \ is \ \ disjoint\ \ with \ \ A_m(m \not= n)

  • 속성

    • P(Ac)=1−P(A) P(A^c) = 1 - P(A)

      • Proof

        • 1=P(S)=P(A⋃Ac)=P(A)+P(Ac)  sinceA⋂Ac=∅ 1= P(S) = P(A \bigcup A^c) = P(A) + P(A^c) \ \ since A \bigcap A^c = \varnothing

    • If A⊆B A \subseteq B , then P(A)≤P(B) P(A) \leq P(B)

      • Proof

        • B=A⋃(B⋂Ac) B = A \bigcup (B \bigcap A^c) , disjoint

        • P(B)=P(A)⋃P(B⋂Ac) P(B) = P(A) \bigcup P(B \bigcap A^c)

    • P(A⋃B)=P(A)+P(B)−P(A⋂B) P(A \bigcup B) = P(A) + P(B) - P(A \bigcap B)

      • Proof

        • P(A⋃B)=P(A⋃(B⋂Ac))=P(A)+P(B⋂Ac)?=P(A)+P(B)−P(A⋂B) P(A \bigcup B) = P(A \bigcup (B \bigcap A^c)) = P(A) + P(B \bigcap A^c) ?= P(A) + P(B) - P(A \bigcap B)

        • P(B)=P(A⋂B)+P(Ac⋂B) P(B) = P(A \bigcap B) + P(A^c \bigcap B) => True

        • since, P(A⋂B),P(Ac⋂B) P(A \bigcap B), P(A^c \bigcap B) are disjoint, union is B

      • 포함배제의 원리, inclusion-exclusion

    • P(A1⋃A2⋃⋯⋃An)=∑i=1nP(Ai)−∑i<jP(Ai⋂Aj)+∑i<j<kP(Ai⋂Aj⋂Ak)−⋯+(−1)n+1P(Ai⋂⋯⋂An) P(A_1 \bigcup A_2 \bigcup \cdots \bigcup A_n) = \sum_{i=1} ^n P(A_i) - \sum_{i \lt j} P(A_i \bigcap A_j) + \sum_{i \lt j \lt k} P(A_i \bigcap A_j \bigcap A_k) - \cdots + (-1)^{n+1}P(A_i \bigcap \cdots \bigcap A_n)

몽모르트 문제 : 드 몽모르트가 만든 문제

  • 도박에서 처음 나온 문제

  • 1부터 n까지 적혀있고 각 수마다 한 장만 존재하는 카드 뭉치가 존재

  • 카드를 셔플 후, 카드 뭉치에 있는 카드의 순서와 카드의 값이 일치하는 경우 승리

  • 포함배제의 원리를 이용하여 푸는 것이 가장 쉽다

  • P(Aj)=1n P(A_j) = {1 \over n} , j카드가 j-th에 있을 확률, 이 때 j에 대한 식이 아니다

  • P(A1⋂A2)=(n−2)!n!=1n(n−1) P(A_1 \bigcap A_2) = { (n-2)! \over n!} = {1 \over n(n-1)} , n개의 카드 중 1과 2가 각각 첫번째와 두번째에 있어야 함

  • P(A1⋂⋯⋂AK)=(n−k)!n! P(A_1 \bigcap \cdots \bigcap A_K) = { (n-k)! \over n!}

  • P(A1⋃⋯⋃AK)=n⋅1n−n(n−1)2!1n(n−1)+n(n−1)(n−2)3!1(n(n−1)(n−2)−⋯=1−12!+⋯+(−1)n1n!=1−1e P(A_1 \bigcup \cdots \bigcup A_K) = n \cdot {1 \over n} - {n(n-1) \over 2! }{1 \over n(n-1)} + { n(n-1)(n-2) \over 3! }{1 \over (n(n-1)(n-2)} - \cdots \\ = 1 - {1 \over 2!} + \cdots + (-1)^n {1 \over n!} = 1 - {1 \over e}

  • 테일러 급수와 비슷한 모양

Previous14 ThuNext12 Tue

Last updated

Was this helpful?