12 Tue

TIL

[AI 스쿨 1기] 6주차 DAY 2

선형회귀(Linear Models for Regression)

출처 : https://github.com/sujiny-tech/k-digital-training-AI-dev/blob/main/Machine-Learning-basics/Linear%20Models%20for%20Regression.md

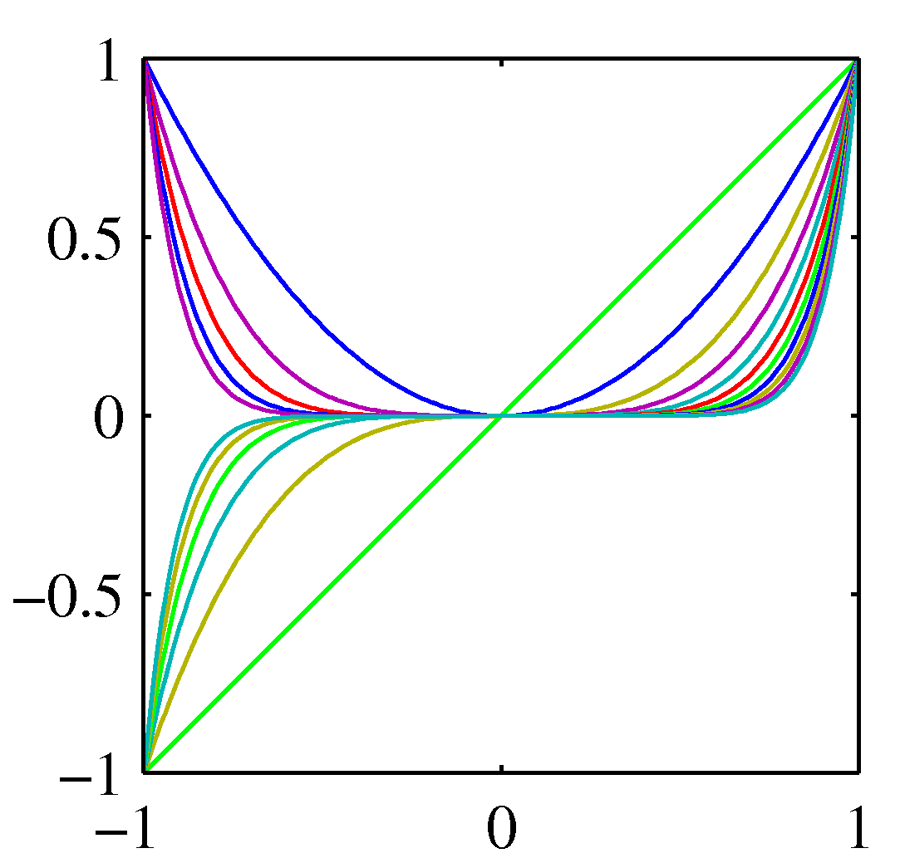
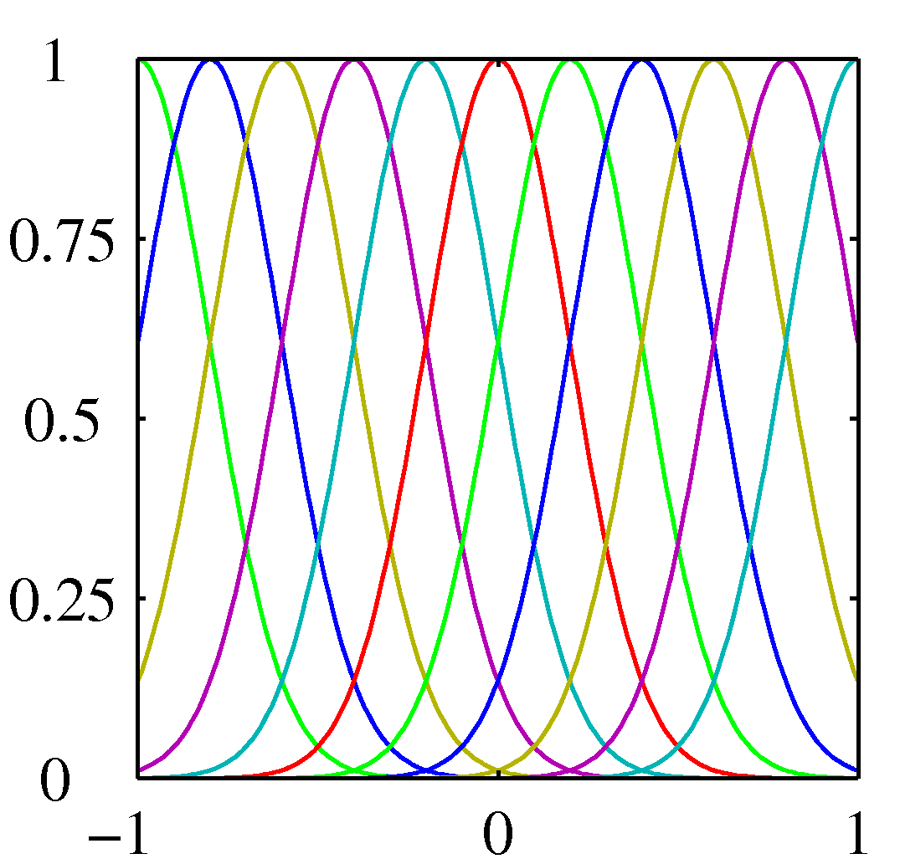
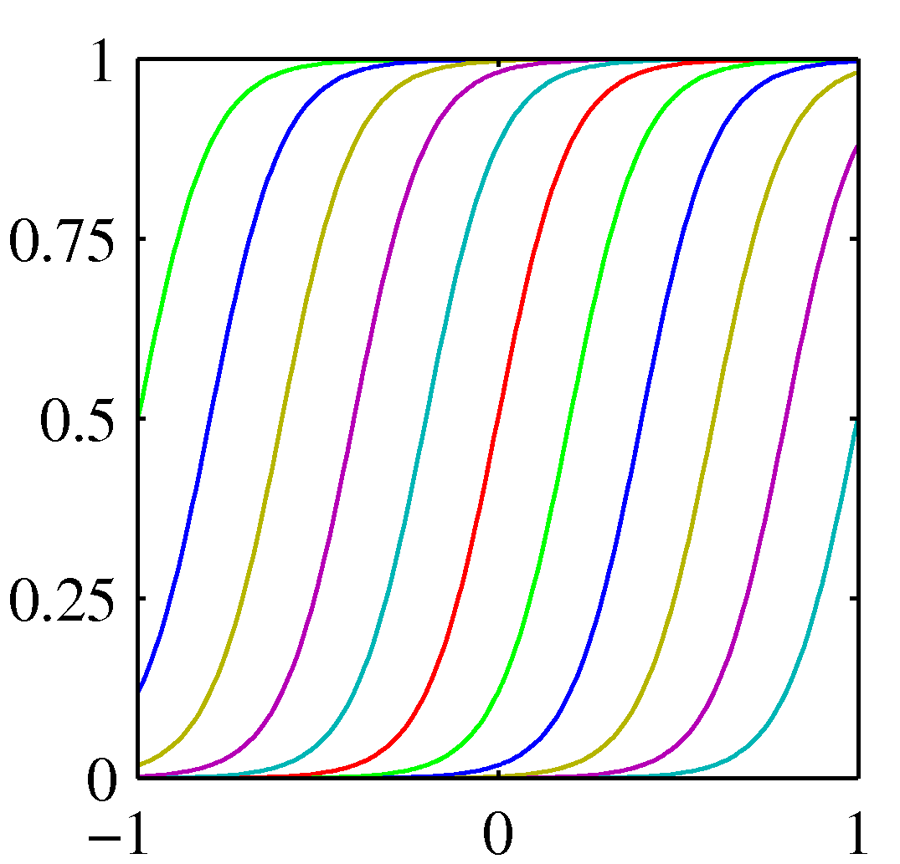
선형 기저 함수 모델

• 가장 단순한 모델

  

  

  • x에 관한 비선형 함수는 다음과 같다.

    

    

    기저함수(basis function) :

• 몇가지 기저 함수

  • 다항식(polynomial) 기저함수

    

  • 가우시안 기저함수

    

  • 시그모이드(sigmoid) 기저함수

    

    

    

    왼쪽부터 다항식 기저함수, 가우시안 기저함수, 시그모이드 기저함수

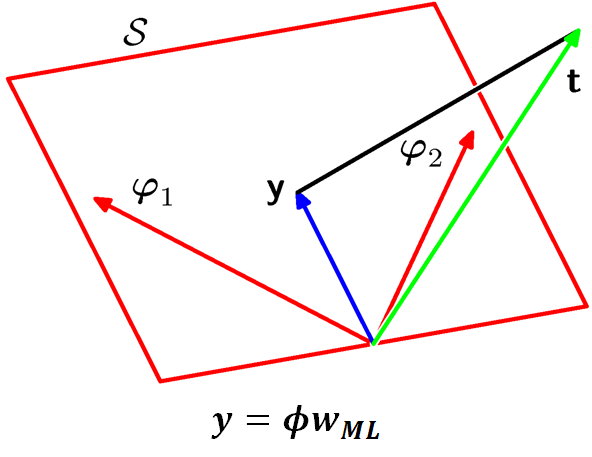
최대우도와 최소제곱법(Maximum Likelihood and Least Squares)

• 가우시안 노이즈가 포함된 타겟 t

  

  : 결정론적 함수(deterministic)

  : 노이즈 확률변수

• t의 분포

  

  • 제곱합이 손실함수로 쓰이는 경우, 새로운 x가 주어졌을때 t의 최적 예측 값은 t의 조건부 기댓값 (이전 강의)

    t가 위의 분포를 따르는 경우 조건부 기댓값

    

• 최대우도추정법을 통한 최적의 w 구하기

  • 입력 값 :

  • 출력 값 :

  • 우도함수

    

  • 로그 우도함수

    

    

    로그우도함수 최대화시키는 w값 = 로 주어진 제곱합 에러함수 최소화시키는 값❗

  • w에 대한 기울기 벡터

    

    w의 최적값 : (normal equations)

    의 Moore-Penrose pseudo-inverse :

    디자인 행렬(design matrix)

    

  • normal equations 유도하기

    

    

    전개하면,

    

    

    

    • design matrix의 모든 열이 선형 독립이면, 존재❗ (항상성립하진 않지만 많은 경우에 성립하며, 성립하지 않은 경우에 대해 성립하도록 데이터 조절 가능)

  • 구한 에러함수를 편향 파라미터(bias parameter) 로 표현하면

    

    

    

    이때 는 의 차이를 보정해주는 역할❗

    위의 로그우도함수 식에서 β에 대해 편미분을 통해 최적값을 구할수 있음

    

• 기하학적 의미

  • span, range, projection 복습 > 선형대수

  • 행렬 A에 관한 사영

    

    

온라인 학습 (Sequential Learning)

• 데이터의 사이즈가 너무 크면 계산이 어려움 -> 여러 대안이 존재, 그 중 하나

• 갖고있는 학습데이터를 조금 나눠서 조금씩 업데이터 진행

• 데이터가 아무리 크더라도 어느정도 모델 학습 가능

• 그 중 많이 쓰이는 Stochastic gradient decent

  • 에러함수가 라 할때, 으로 학습 진행

    제곱합 에러함수인 경우,

    

    으로 표현

• 시간은 많이 걸리더라도, 메모리에 대한 부담은 ↓

✨관련 실습

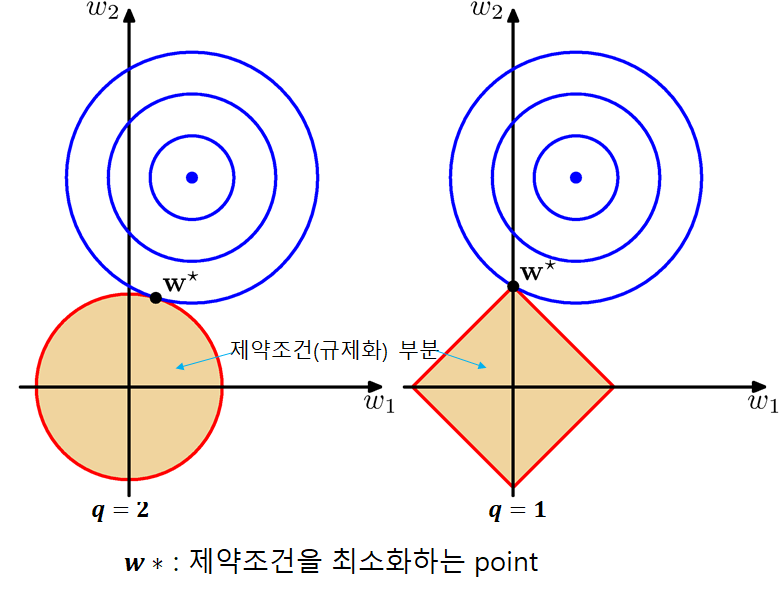
규제화된 최소제곱법(Regularized Least Squares)

• 에러함수의 가장 단순한 형태

  

  lambda에 의해 규제화 컨트롤

  

  

  

  w에 대해 미분하고, 정리하면 w의 최적값 ->

• 일반화된 규제화

  

  • 이때, 제약조건을 두어 생각하면 (constrained minimization 문제로 나타내면),

    를 만족하면서 를 최소화시키는 해 찾기 !

    

편향-분산 분해(Bias-Variance Decomposition)

• 모델 과적합에 대한 이론적인 분석

• 제곱합 손실함수가 주어졌을때의 최적 예측값

  

• 손실함수의 기댓값

  

  제한된 데이터셋만 알아서는 최적 예측값 h(x)를 알수 없다.

  따라서 모델의 불확실성을 표현하기 위해서는 베이지안/빈도주의 방법이 있음

  • 베이지안 방법은 모델 파라미터 w의 사후확률분포를 계산

  • 빈도주의 방법은 w의 점추정값을 구하고, 여러 데이터셋에 대해 발생하는 평균적인 손실을 계산하는 가상 실험을 통해 점추정값의 불확실성을 해석❗

/ 빈도주의 방법...

• 특정 데이터 셋 D에 대한 손실

  

• 손실 함수의 기댓값

  

• 여러 개(L개)의 데이터셋이 주어졌을 떄, 이 값들의 평균?

  

  

  에 대해 변형하면

  

  따라서,

  

• 정리하면,

  • 

  • 

  • 

  • 자유도 ↑, 복잡도 ↑, var ↑, bias^2 ↓ (var, bias : trade-off)

  • 모델학습에 적절한 모델복잡도(자유도)를 가질수 있도록 해야 좋은 모델(새로운 데이터에 대해 너무 과적합되지 않은 결과를 낼 수 있는 모델)❗

베이지안 선형회귀(Bayesian Linear Regression)

• 위에서 처럼 빈도주의방법으로는 모델의 불확실성을 나타내기 힘듦❗ 베이지안 선형회귀를 통해 훨씬 더 불확실성을 깔끔하게 다룰 수 있음❗

• 파라미터 w의 사전확률

  

• 우도

  

• 사후확률

  

  (using 가우시안 분포를 위한 베이즈 정리)

  

  

  

  사전 확률의 공분산 이라고 가정하면,

  , 수렴

  mN에 대입하면,

  (normal equations)

• 사후확률의 로그값

  

• 베이지안 방법은 빈도주의보다 일반적이고, 강력한 방법론❗

• 예측값의 분포를 구할 수 있음❗

• 예측 분포 (Predictive Distribution)

  • 새로운 입력 x이 주어졌을 때, t 예측

    

  • 이전 결과 적용하면,

    

✨ 공부하면서 참고한 사이트

[Statistics 110]

Present Part [2 / 34]

2강- 해석을 통한 문제풀이 및 확률의 공리 (Story Proofs, Axioms of Probability)

10명을 4명과 6명으로 나누어 두 팀을 만드는 경우의 수

10명 중 4명을 뽑은 경우의 수 ${10 \choose 4 }$ 와 같다. 4명을 뽑으면 6명이 자동으로 결정되기 때문이다. 또한 이는 10명 중 6명을 뽑은 경우의 수와 같으며 증명하지 않아도 개념적으로 ${10 \choose 4 } = {10 \choose 6 }$ 라는 것을 알 수 있다.

10명을 5명과 5명으로 나누어 두 팀을 만드는 경우의 수

이는 10명 중 5명을 뽑는 경우의 수${10 \choose 5 }$와 같은데 여기서 1/2 를 해야한다. 왜냐하면 5명을 뽑으면 자동으로 5명이 결정되는 경우에서 이미 반대편에서도 동시에 5명을 뽑는 경우의 수가 같이 카운트 되기 때문이다. 따라서 중복으로 카운트된 것을 제하기 위해 1/2을 곱해야 한다.

이렇게, 항상 경우를 잘 보고 중복의 여부를 잘 판단해야 한다.

복원 가능, 순서 미고려 ${n+k-1 \choose k}$

다음의 경우의 수가 맞는지를 결정하기 위해 몇가지 케이스를 생각해본다.

• k = 0일때,${n-1 \choose 0}$ = 1

  • 아무것도 결정하지 않을 때의 경우의 수는 1이 맞다. 0! = 1

• k = 1일때, ${n \choose 1}$= n

  • n개 중 1개를 뽑는 경우의 수는 n개

• n = 2일때, ${k+1 \choose k}$= ${k+1 \choose 1}$= k+1

n개의 구분 가능한 박스 안에 k개의 구분 불가능한 입자를 넣는 방법

• ${n+k-1 \choose k}$

• n = 4, k= 6 일때

  • 3 / 0 / 2 / 1

  • ooo||oo|o => o of k and | of n-1

  • 이는 n+k-1 개의 위치에서 k개의 점을 위치시키는 개념과 동일

  • 점의 위치가 결정되면 분리선의 위치가 자동으로 결정된다

• n = 2일때 => 동전을 뒤집는 상황

  • 앞면과 뒷면이 공정한 확률을 가지면 4가지 경우를 가진다

  • 동전 한 개를 두번던지고 이 동전이 절대 구별할 수 없다고 가정하면 실제로는 3가지 경우(?)

이야기 증명(Story Proof)

• 해석에 의한 증명

  • ex)초반에 이야기한 10개중 4개를 뽑을 확률 = 10개중 6개를 뽑을 확률

  • 팩토리얼을 가지고 비교하지 않았음

• n${n-1 \choose k-1}$= k${n \choose k}$

  • n명중에서 동아리에 들어갈 k명의 사람을 고르고 이 중 대표 1명을 뽑을 경우의 수

  • 그러나 이는 해석적으로 다르게 말할 수 있다

  • n명중에서 대표 1명을 뽑고 나머지 중에서 k-1명의 사람을 뽑을 경우의 수

• ${m+n \choose k}$= $\sum^k_{j=0} {m\choose j} {n \choose k-j}$: 방데르몽드 항등식

  • 이를 증명하려면 팩토리얼을 사용하거나 이항 정리를 이용해야 한다

  • 좌변 : m+n개 중 k개를 고르는 것

  • 우변 : m+n개를 m개와 n개의 그룹으로 나눈 뒤 k명이 되도록 뽑는 것. (이 때 m에서 0명이 뽑히면 n명에서는 자동으로 k명이 뽑히고, m명에서 1명이 뽑히면 n명에서 k-1명이 뽑힌다)

확률

지금까지는 모두 동일한 확률이 발생한다고 가정하고 문제를 해결했으며 그 경우의 수도 유한하다고 가정한 뒤 확률을 정의했다.

간단하지 않은 확률의 정의는 다음과 같다.

• 확률 공간에는 두 개의 성분 S와 P가 있다.

• S는 표본 공간이며 모든 실험이 이루어 질 수 있는 공간.

• P는 함수이다.(끄러나 f(x) = x+ 3 같은 함수는 아니다) 어떤 사건을 입력으로 하는 함수이다. P의 정의역은 S의 부분집합이다.

• S의 부분집합 A가 있을 때 P(A)는 0부터 1 사이의 수이며, 일반적인 확률은 0과 1사이의 기준이다. 이 때 P를 정의하기 위한 두 가지 정리는 다음과 같다.

  • P($\varnothing$) = 0, P(S) = 1

    • 모든 가능한 결과의 집합이 S일 때, 발생할 수 없는 불가능한 사건이 $\varnothing$ 이다.

    • $P (\cup^\infty_{n=1}) = \sum^\infty_{n=1}P(A_n) \ \ \ \ if \ \ A_n \ \ is \ \ disjoint\ \ with \ \ A_m(m \not= n)$

  • 확률의 모든 정의와 규칙은 이 두 정리로부터 파생된다.