11 Mon

TIL

[AI 스쿨 1기] 6주차 DAY 1

출처 : https://github.com/sujiny-tech/k-digital-training-AI-dev/blob/main/Machine-Learning-basics/Probability%20Distributions_II.md

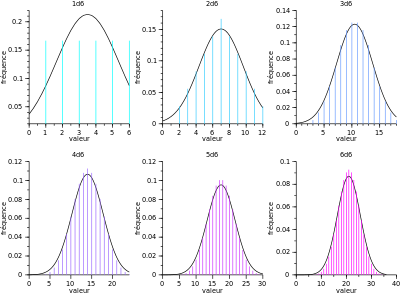
가우시안 분포(Gaussian Distribution)

• 가우시안 분포가 일어나는 여러가지 상황

  • 정보이론에서 엔트로피를 최대화시키는 확률분포

  • 중심극한 정리

    

    그림 출처

• 단일 변수 x

  

• D차원 벡터 x

  

  : D차원의 평균 벡터

  : DxD크기를 가지는 공분산 행렬

  평균과 분산으로 주어진게 아니라 위의 형태의 함수를 가지고 있으며 mu, sigma가 파라미터로 주어져있을 때, 확률밀도함수의 평균과 공분산이 mu, sigma가 된다는 것을 유도❗

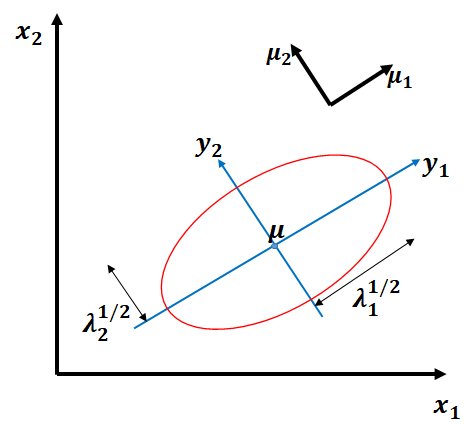
• 가우시안 분포의 기하학적인 형태

  • x에 대한 함수적 종속성은 지수부에 등장하는 이차형식(quadratic form)

    

  • 가 공분산으로 주어진 것은 아니므로 처음부터 이 행렬이 대칭이라고 미리 가정할 필요 x❗

  • 하지만, 선형대수에서 배웠듯 이차형식에 나타나는 행렬은 오직 대칭부분만이 그 값에 기여한다는 사실을 기억하자❗

    

    따라서, 가 대칭행렬인 것으로 간주할 수 있음.

  • 대칭행렬의 성질에 따라서 를 아래와 같이 나타낼 수 있음.

    

    

    

    

    

    

  • 쉽게 구할 수 있음.

    

  • 이차형식은 다음과 같이 표현

    

    

  • 벡터식으로 확장하면

    

    

    y를 벡터들 에 의해 정희된 새로운 좌표체계 내의 점으로 해석 → 이를 기저변환(change of basis) 라 함.

    

    

    

    : standard basis에서의 좌표

    : basis 에서의 좌표

    

• 가우시안 분포의 Normalization 증명

  • 의 확률밀도함수를 구하기 위해서 Jacobian 를 구해야 함❗

    

    

  • 행렬식 는 고유값의 곱으로 나타낼 수 있음

    

  • 따라서, y의 확률밀도함수는 다음과 같음.

    

  • y의 normalization

    

• 가우시안 분포의 기댓값

  • 다변량(multivariate) 확률변수의 기댓값

    • 

    • 

    • 

  • 가우시안 분포의 기댓값 계산

    

    

    z 부분에 대해 정리하면,

    

    

    

    

    

    (부분이 남기때문에)

  • 가우시안 분포의 공분산

    공분산을 구하기 위해 먼저 2차 적률(seconde order moments)를 구함

    

    

    는 DxD 행렬이므로 를 로 치환하면,

    

    

    

    

    

    • 는 개의 행렬 합이며 그 중 에 관해 영행렬이 됨.

      

      ( [ ]안의 식이 odd function이므로)

      따라서,

      

      

      

      

      : 상수부분

      

      

      나머지 부분에 관해서는 odd function의 성질로 사라지며, 마지막 은 별개의 부분으로 적분 앞으로 나옴.

    • 따라서 정리하면, 임.

    • 확률변수의 벡터 x를 위한 공분산은 다음과 같음.

      

      위에서 게산한 결과를 이용하면, ❗

조건부 가우시안 분포(Conditional Gaussian Distribution)

• D차원의 확률변수 벡터 x가 가우시안 분포 를 따른다고 하자. x를 두 그룹의 확률변수들로 나눴을때, 한 그룹이 주어졌을때 나머지 그룹의 조건부 확률도 가우시안 분포를 따르며, 각 그룹의 주변확률변수 또한 가우시안 분포를 따름.

  

  • : M개의 원소를 가짐.

  평균벡터 :

  공분산 행렬 : 의 형태를 가진다고 하자.

  공분산의 역행렬 : ( 정확도 행렬(precision matrix)를 사용하는 것이 수식을 간편하게 함)

  

  • 지수부의 이차형식을 파티션을 사용해서 전개하면 다음과 같다.

    

• 완전제곱식(Completing the Square) 방법

  • 변형해서 함수g(xa)를 찾는 것이 목표❗

  라 하며, 이때 이 함수의 적분이 1이고, α는 와 독립적임.

  

  α는 에 관해 적분했으므로, 의 주변확률.

  이므로, ❗

  즉, 함수 를 찾는 것이 목표

  이때, 이차 형식을 완전제곱식 형식으로 변형하면,

  

  ❗

  

  이때, b는 normalize하기 위한 상수

  에 해당하는 부분 :

  α에 해당하는 부분 :

• 가우시안 분포의 지수부

  

  

  이때, 가운데 두 값은 transpose하면 같은 값이고, 마지막항은 x와 관계없으르모 상수 취급

  이차항을 통해 공분산 행렬을 구하고, 이를 통해 일차항의 계수인 평균벡터 mu를 구할 수 있음❗

• 앞서 파티션한 부분에서

  의 이차항 :

  따라서 공분산 ->

  이를 통해 일차항을 정리해서 계수를 통해 평균벡터를 구하면,

주변 가우시안 분포(Marginal Gaussian Distributions)

• 목표❗

  

• 전략

  

  

  

  

  

  

  

  이때, β는 에 관한 적분 값.

  이를 완전제곱식으로 변형해서 이전의 방법처럼 공분산과 평균벡터 구할 수 있음❗

• 파티션을 위한 이차형식을 다시 살펴보면, 전체 16개 항 중 를 포함한 항은 7개이며 를 포함한 항은 5개

  정리하면,

  

• 를 완전제곱식 형태로 만들기

  치환해서 를 빼주고 더해주면 다음과 같이 변형됨.

  

  이는 공분산 에만 종속되며, 에는 독립이므로 앞서 설명한 의 지수부에 집중하면 됨❗

• 따라서, 에 관해 정리하면,

  

  

  

  

  

  

  • 

  • by Schur complement

가우시안 분포를 위한 베이즈 정리(Bayes' Theorem for Gaussian Variables)

• 주어진 값

  • 

  • 

    • 의 평균은 x의 선형함수

    • 의 공분산은 x와 독립

• 구할 값 :

• 를 위한 결합확률분포 (이를 통해 공분산, 평균벡터 계산)

  

  

  • z의 이차항 정리 (공분산)

    

    

    

    

  • z의 이차항 정리 (평균벡터 -> 일차항)

    

    

  • 주변 가우시안 분포 결과 를 적용하여 y에 관한 주변확률분포의 평균과 공분산은 다음과 같음.

    

    

  • 조건부 가우시안 분포 결과 를 적용하여 조건부 확률 의 평균과 공분산은 다음과 같음.

    

가우시안 분포의 최대우도(Maximum Likelihood for the Gaussian)

• 가우시안 분포에 의해 데이터 가 주어졌을 때 우도를 최대화하는 파라미터 값(평균, 공분산) 찾기❗

  • 로그 우도 함수

    

  • 우도를 최대화하는 평균벡터

    치환

    

    

    

  • 우도를 최대화하는 공분산 행렬

    

    

    

    

    

    

    

    

    

    • 이해하기

      • 역행렬 연산이 일대일함수를 정의하기 때문에, 성립함❗

가우시안 분포를 위한 베이지안 추론(Bayesian Inference for the Gaussian)

• MLE방법은 파라미터들의 하나의 값만 구했다면, 파라미터의 확률분포 자체를 구할 수 있음❗

• 우도함수 와 사전확률 를 통해 의 사후확률 구하기❗

  • 분산은 주어졌다고 가정, 단변량 가우시간 확률변수 x의 μ를 베이지안 추론을 통해 구한다.

  • 우도함수

    

  • 사전확률

    

  • 사후확률

    

    

    

    

    앞에서 사용했던 완전제곱식 방법을 통해 보일 수 있음❗